6G Communication Systems Utilizing Intelligent Reflective Surfaces for Improved Data Rates Based on AI

Jehan Kadhim Shareef Al-Safi; Abbas Thajeel Rhaif Alsahlanee

doi:10.69709/CAIC.2025.100022

Abstract

Intelligent Reflecting Surfaces (IRSs) are essential for energy-efficient 6G networks; however, enhancing their performance to attain both elevated data rates and energy efficiency continues to be a formidable challenge. This paper uses artificial intelligence (AI) to solve this problem by creating a new AI-based optimization algorithm called Dynamic and Static Particle Swarm Optimization (DS-PSO). The suggested AI method intelligently learns the best phase-shift settings for IRS elements, balancing exploration and exploitation in real time to get the best signal-to-noise ratio at the receiver. The simulation results show that our method works, with the AI-optimized IRS model being up to 269% more energy-efficient than a standard IRS at 10 bits/s/Hz. This study highlights the considerable potential of AI algorithms in navigating the complex trade-offs of next-generation communication systems, establishing our model as a robust solution for sustainable 6G connectivity.

1. Introduction

The intelligent reflecting surface (IRS) has emerged as a promising technology for sixth-generation (6G) wireless communication systems by improving propagation environments and mitigating the effects of high path loss in line-of-sight (LOS) conditions [1]. An intelligent radio environment has recently been developed to meet the stringent criteria for communication and sensing imposed by future 6G systems [2]. In this approach, the digitally-controlled metasurface, also known as a reconfigurable intelligent surface (RIS) or IRS, wirelessly alters the propagation environment to enhance wireless communication and radar sensing [3].

Metasurfaces are a novel type of functional material containing artificially periodic or quasiperiodic structures on sub-wavelength length scales [4,5]. The active elements in IRS metasurface unit cells allow for the electrical adjustment of electromagnetic waves, which means they can be programmed [6,7]. Metasurfaces show negative permeability and permittivity [8]. Metasurfaces may change electromagnetic waves from microwaves to visible light. Wireless link quality varies over time due to the unpredictable nature of radio propagation. During the propagation of electromagnetic waves, free-space line-of-sight (LOS) paths, reflections, refractions, signal absorption, and diffraction caused by physical objects render wireless channels highly dynamic [9]. The ability of the IRS to manipulate electromagnetic waves in real time opens up new possibilities, shifting the wireless communication design paradigm from “adapting to wireless channels” toward “actively shaping wireless channels”[9,10]. In particular, IRS can achieve desirable functions by dynamically regulating phase shifts using low-cost reflecting elements, including multi-antenna/MIMO (multiple-input multiple-output) channel rank improvement, environment obstacle avoidance, and reshaping channel realizations/distributions [11].

Improved communication system performance is possible when transmit beamforming is used with an IRS that uses a phase-shift design [12,13]. Transmit beamforming can also synthesize multiple beams toward existing users and targets [12,13,14].

The creation of the IRS reflection pattern (passive beamforming) requires channel state information (CSI) for the subchannels between wireless transceivers and the IRS [15]. The IRS cannot detect the incident signal because it is passive, making the estimation process more complex than in other wireless communication systems [16]. Furthermore, prior research has broadened the scope of investigation to incorporate general channel effects, such as fading, alongside practical imperfections, including transceiver misalignment, phase inaccuracies, and interference from mobile users [17,18]. In contrast, dynamically optimizing the phase can strengthen the communication signal [19].

Multiple performance metrics, such as spectral efficiency (SE), transmit power, sum rate, throughput, security, and others, have been the focus of substantial research into the use of IRS in wireless communication [20]. In addition, the literature has discussed the energy efficiency (EE) metric as a means of assessing the performance of IRS within wireless communication networks, as in [2,10,20].

We have performed multiple studies on the application of AI-driven optimization for recommender systems, communications, and networks, including [21,22,23,24,25,26].

The goal of this study is to improve the energy efficiency of an IRS-enabled system, which will improve transmission performance in 6G wireless networks without lowering data rate requirements. Using AI techniques to reprogram the IRS system can make the new models work better. To make the standard IRS model work better, an AI algorithm called DS-PSO (dynamic and static particle swarm optimization) has been suggested. The IRS system can handle the most data at the fastest speeds while using the least amount of energy. So, the choice between standard IRS and optimized IRS (IRS⁰) models affects how much energy they use and how fast they send data. The data rate affects how energy-efficient an IRS is. Data rate and energy efficiency are both increased by the proposed optimization algorithm. However, for the (IRS⁰) model, the necessary energy-efficiency improvement is determined by the target data rate. As a result, the energy efficiency and data rates of the (IRS⁰) model are examined using the mathematical formulations created in this work.

IRS-assisted communication has a solid foundation thanks to the literature currently in publication, but there are still a number of unmet research needs, which this work attempts to address. First off, a lot of research concentrates on throughput or spectral efficiency optimization, but it doesn’t thoroughly examine the crucial trade-off between high data rates and energy efficiency (EE) in multi-IRS 6G scenarios. Second, although algorithms like Genetic Algorithm (GA) and standard PSO have been used, they frequently result in premature convergence to local optima in the intricate, high-dimensional IRS phase-shift optimization problem, suggesting the need for more reliable hybrid optimization strategies. Lastly, there is a lack of a standardized benchmarking framework in the literature that uses energy efficiency versus data rate as a useful performance metric to compare the suggested models with standard IRS, SISO, and a number of well-known schemes (such as single, double, triple IRS, PSO-IRS, and GA-IRS). This paper seeks to address these shortcomings by presenting a novel AI-driven hybrid algorithm and a comprehensive comparative performance assessment.

The main new ideas in this paper are: (1) We introduce a novel hybrid Dynamic and Static Particle Swarm Optimization (DS-PSO) algorithm, meticulously designed to rectify the deficiencies of traditional optimizers in the complex, non-convex realm of IRS phase-shift optimization. Its hybrid topology does a better job of balancing exploration and exploitation. (2) A complete analytical framework is created for the (IRS⁰) model to find the most important performance metrics for energy efficiency and data rate. (3) We perform a comprehensive simulation study that compares the proposed model to a standard IRS, a SISO baseline, and the most recent works in the field (such as PSO-IRS, GA-IRS, and multi-IRS configurations). (4) We show that the (AI-IRS⁰) model works much better than a standard IRS when there is a lot of data, with energy efficiency improvements of up to 269%. This shows that it could be a key technology for 6G networks.

The rest of this paper is set up like this. In Section 2, we talk about the system model, the analytical performance framework, and the suggested AI-based optimization method. In Section 3, we show the results of the simulation and how they compare to each other. Section 4 talks about problems that come up when putting things into practice. Lastly, Section 5 will talk about the conclusion and what needs to be done next.

2. Materials and Methods

This section outlines the system model, analytical performance framework, and the proposed AI optimization algorithm used to evaluate the enhanced IRS-aided 6G communication system.

2.1. System Model

Here, we focus on one-to-one transmissions, where the source and destination each have a single antenna, where $h_{s d} \in C$ represents the deterministic flat-fading channel, while the destination receives a signal as in (1).

(1)

y = h_{s d} \sqrt{p} s + n

where

n \sim N c (0, σ^{2})

, denotes the noise at the receiver,

s

stands for the unit-power information signal, and

p

is the transmit power. Antenna gains are absorbed into the channel coefficients for notational simplicity. Equation (2) describes the capacity of this SISO channel, which is (single-input-single-output).

(2)

R_{S I S O} = {l o g}_{2} (1 + \frac{p | h_{s d} |^{2}}{σ^{2}})

A higher transmission capacity during wireless communication can be achieved by using additional technologies. An IRS is one such technology that can enhance the data transmission capacity of wireless communication systems. IRSs can outperform relays at processing deterministic flat-fading channels, channel estimation, and frequency-selective fading. In terms of performance, deterministic flat-fading channels achieve the best performance [27].

For clarity and ease of mathematical manipulation, we employ deterministic flat-fading channels in our simulations and analysis. However, real-world wireless environments frequently experience frequency-selective fading. This makes it more difficult to compare the performance of IRS and relays.

One of the best features of relays is their ability to perform tasks like equalization and amplification, which can reduce inter-symbol interference brought on by fading that only impacts specific frequencies. An IRS cannot perform this type of active equalization since it is passive. It works well in wideband systems if it can make a frequency-flat response or if it uses more advanced, frequency-selective phase shift designs, which is an area of active research. So, even though IRS technology has big benefits in terms of power efficiency and possible spatial gain over relays in flat-fading channels, using it in environments with strong frequency selectivity needs to be thought about carefully and may involve trade-offs compared to active relays. This indicates a promising avenue for future research.

This paper examines IRS properties and develops an optimized IRS model. Subsequently, we compare the standard and ( ${I R S}^{o}$ ) models to ascertain their strengths and weaknesses. To conduct this study, we created a comprehensive transmission diagram in the wireless communication system using either the standard IRS or the proposed ( ${I R S}^{o}$ ), as shown in Figure 1.

Figure 1: Standard IRS model/improved IRS model aided transmission. — **Figure 1:** Standard IRS model/improved IRS model aided transmission.

2.1.1. The Transmission with the Support of the Standard IRS Model (IRS)

Discrete elements $N$ exist in the standard IRS model (IRS), as shown in Figure 1, where $h_{s r} \in C^{N}$ represents the source-to-IRS deterministic channel, and [ $h_{s r}$ ] $n$ the $n$ th element; $h_{r d} \in C^{N}$ . This specifies the channel that must be specified for the IRS to communicate with the destination.

(3)

Θ = α d i a g (e^{j θ 1}, \dots, e^{j θ N})

where

α \in [0,1]

is the reflection coefficient at the fixed amplitude;

θ_{1}, θ_{2}, \dots, θ_{N}

, these are the phase-shift parameters that may be enhanced with IRS. The final destination’s received signal within the IRS was calculated using the system model obtained in [28], which was previously used in [27,29,30], as in (4).

(4)

y_{I R S} = (h_{s d} + h_{s r}^{T} Θ h_{r d}) \sqrt{p s} + n

where using the same definitions for

p,

s

, and

n

as used in the SISO case. With IRS-supported transmissions, channel estimation is non-trivial since the destination has perfect knowledge of the channels, and the phase-shift parameters can be enhanced. However, [31] describes several contemporary techniques addressing this challenge. Specifically, the IRS-supported network has a channel capacity as in (5).

(5)

R_{I R S} (N) = \underset{θ_{1}, \dots, θ_{N}}{m a x} \log_{2} (1 + \frac{p {|h_{s d} + h_{s r}^{T} Θ h_{r d}|}^{2}}{σ^{2}})

(6)

R_{I R S} (N) = \log_{2} (1 + \frac{p {(|h_{s d}| + α \sum_{n = 1}^{N} |{{[h_{s r}]}_{n} [h_{r d}]}_{n}|)}^{2}}{σ^{2}})

The rate expression in (5) will be obtained from the carrying capacity of a channel generating additive white Gaussian noise for any $Θ$ . Take note that the essential factor is $h_{s r}^{T} Θ h_{r d} = α \sum_{n = 1}^{N} e^{j θ n} {{[h_{s r}]}_{n} [h_{r d}]}_{n}$ . Following the same standard procedure as in [32,33], the maximum rate, which represents the capacity, is achieved whenever the phase shifts are chosen as $θ_{n} = a r g (h_{s d}) - a r g ({[h_{s r}]}_{n} {[h_{r d}]}_{n})$ to make each term in the sum have the same phase as $h_{s d}$ .

2.1.2. The Transmission with the Support of the Optimized IRS Model ( I R S o )

In this paper, we present an improved version of the IRS model; it is the ( ${I R S}^{o}$ ) model (shown in Figure 1) utilizing one of the available optimization algorithms to surpass the performance and capabilities of the IRS.

The enhanced, as in the (7) diagonal matrix, shows the properties of the ${I R S}^{o}$ , just like in the IRS, except for the value of N.

(7)

Θ^{o} = α d i a g (e^{j θ 1}, \dots, e^{j θ N^{o}})

where

N^{o}

, are the

N

enhanced, phase-shifting variables that can be represented by

θ_{1}, θ_{2}, \dots, θ_{N^{o}}

, these optimize through

{I R S}^{o}

. Furthermore, the final destination received the enhanced signal within

{I R S}^{o}

, will be as in (8).

(8)

y_{I R S}^{o} = (h_{s d} + h_{s r}^{T} Θ^{o} h_{r d}) \sqrt{p^{o} s^{o}} + n^{o}

where

p^{o}

, is the enhanced transmit power,

s^{o}

, is the unit-power information’s enhanced signal, and the enhanced receiver noise will be represented by

n^{o} \sim N c (0, σ^{2})

. To analyze how the optimized model for the IRS affects the enhanced channel capacity in a network, we will use the expressions (9) and (10).

(9)

R_{{I R S}^{o}}^{o} (N^{o}) = \underset{θ_{1}, \dots, θ_{N^{o}}}{m a x} \log_{2} (1 + \frac{p^{o} {|h_{s d} + h_{s r}^{T} Θ^{o} h_{r d}|}^{2}}{σ^{2}})

(10)

R_{{I R S}^{o}}^{o} (N^{o}) = {l o g}_{2} (1 + \frac{p^{o} {(|h_{s d}| + α \sum_{n^{o} = 1}^{N^{o}} |{{[h_{s r}]}_{n^{o}} [h_{r d}]}_{n^{o}}|)}^{2}}{σ^{2}})

Although the analysis in this paper simplifies by assuming deterministic channels, extending it to fading channels with complete channel information is straightforward. We need only consider predictions of the rate equations in (6) and (10). In light of this, all the conclusions also hold in this case.

2.2. Performance of Analytics

Here, we analyze the three achievable rates discussed in the previous section. Uniquely, the phases of the channel elements ignore only the amplitudes used in the expressions. From now on, the notation $|h_{s d}| = \sqrt{β_{s d}}, |h_{s r}| = \sqrt{β_{s r}}, |h_{r d}| = \sqrt{β_{r d}}$ , and $\frac{1}{N} \sum_{n = 1}^{N} |{[h_{s r}]}_{n} {[h_{r d}]}_{n}| = \sqrt{β_{I R S}}$ , will be introduced as a means of brevity within the IRS. However, the same notations will have different values with the ${I R S}^{o}$ compared to the IRS, as follows $|h_{s d}^{o}| = \sqrt{β_{s d}^{o}}, |h_{s r}^{o}| = \sqrt{β_{s r}^{o}}, |h_{r d}^{o}| = \sqrt{β_{r d}^{o}}$ , and $\frac{1}{N^{o}} \sum_{n^{o} = 1}^{N^{o}} |{[h_{s r}^{o}]}_{n^{o}} {[h_{r d}^{o}]}_{n^{o}}| = \sqrt{β_{{I R S}^{o}}^{o}}$ , where these notations are used to represent the ${I R S}^{o}$ . The equations (2), (6), and (10) must be reformulated for more compact forms.

(11)

R_{S I S O} = {l o g}_{2} (1 + \frac{p β_{s d}}{σ^{2}})

(12)

R_{I R S} (N) = {l o g}_{2} (1 + \frac{p {(\sqrt{β_{s d}} + N α \sqrt{β_{I R S}})}^{2}}{σ^{2}})

(13)

R_{{I R S}^{o}}^{o} (N^{o}) = {l o g}_{2} (1 + \frac{p^{o} {(\sqrt{β_{s d}^{o}} + N^{o} α \sqrt{β_{I R S}^{o}})}^{2}}{σ^{2}})

Equality will be obtained for $N = 0$ with the IRS and for $N^{o} = 0$ with ${I R S}^{o}$ , where $R_{IRS} (N)$ is an increasing function of $N$ , while $R_{{I R S}^{o}}^{o} (N^{o})$ is an increasing function of $N^{o}$ . It is evident that $R_{{I R S}^{o}}^{o} (N^{o}) > R_{IRS} (N) \geq R_{SISO}$ . As mentioned in [29] and elaborated on in [27,34], the rate increases as $O ({l o g}_{2} (N^{2}))$ when $N$ becomes large. For this reason, for values of $N$ , the exponential growth rate presented in this paper is $O ({l o g}_{2} ({N^{o}}^{2}))$ . Consequently, it is not simple to evaluate the two cases of the IRS and the ${I R S}^{o}$ .

The radio transmission will work enhanced within this paper’s ( ${I R S}^{o}$ ) model compared to the IRS described in the previous literature. The transmission supported by the ( ${I R S}^{o}$ ) model has the highest rate for any $N > N^{o} \geq 1$ if ${β_{s d} > β}_{s d}^{o} > β_{s r}^{o}$ ; because the IRS-supported transmission provides the highest rate for $N \geq 1$ if $β_{s d} > β_{s r}$ compared to transmissions supported with any additional communications equipment [27], in which the ${I R S}^{o}$ model achieves the highest rate in the case of $β_{s d}^{o} \leq β_{s r}^{o} < β_{s d}$ , while the IRS achieves the highest rate in the case of $β_{s d} \leq β_{s r}$ .

(14)

N > \frac{\sqrt{(\sqrt{1 + \frac{2 p β_{r d} β_{s r}}{(β_{s r} + β_{r d} - β_{s d}) σ^{2}}} - 1) \frac{σ^{2}}{p}} - \sqrt{β_{s d}}}{α \sqrt{β_{I R S}}}

(15)

N^{o} > \frac{\sqrt{(\sqrt{1 + \frac{2 p^{o} β_{r d}^{o} β_{s r}^{o}}{(β_{s r}^{o} + β_{r d}^{o} - β_{s d}^{o}) σ^{2}}} - 1) \frac{σ^{2}}{p^{o}}} - \sqrt{β_{s d}^{o}}}{α \sqrt{β_{I R S}^{o}}}

As for the distinction between the transmission supported by the ( ${I R S}^{o}$ ) and IRS; the IRS supports the case that $R_{I R S} (N) > R_{SISO}$ for $N \geq 1,$ yield the highest rate if $R_{I R S} (N) >$ $R_{a c e}$ ; where any additional communications equipment will be represented by $R_{a c e}$ . Because the IRS supports multiple transmissions. $R_{S I S O} > R_{a c e}$ will cause this for $β_{s d} > β_{s r}$ . As a consequence of this, the result will be ${R_{I R S} (N) > R}_{S I S O} > R_{a c e}$ . But, this paper shows that, $R_{{I R S}^{o}}^{o} (N^{o}) > R_{SISO}$ for $N > N^{o} \geq 1$ , in the case supported by the ${I R S}^{o}$ , yields the highest rate if and only if $R_{{I R S}^{o}}^{o} (N^{o}) > R_{I R S} (N)$ achieves. Due to transmission supported by the ${I R S}^{o}$ , ${β_{s r} > β}_{s d}^{o} > β_{s r}^{o}$ always occurs when $R_{S I S O} < R_{I R S} (N)$ . Therefore, the result will be ( ${{R_{{I R S}^{o}}^{o} (N^{o}) > R}_{I R S} (N) > R}_{S I S O}$ ) in this case. It can reduce the inequality, $R_{I R S} (N) >$ $R_{a c e}$ by using (12), if the situation of $β_{s d} \leq β_{s r}$ , with the IRS supporting the transmission. Furthermore, if the case of $β_{s d}^{o} \leq β_{s r}^{o} < β_{s d}$ transmission supported by the ${I R S}^{o}$ , the inequality ${R_{{I R S}^{o}}^{o} (N^{o}) > R}_{I R S} (N)$ can be simplified by using (13).

A LOS between the ${I R S}^{o}$ , and IRSs are required to interpret the results correctly ${I R S}^{o}$ . Since any element in $h_{s r}$ has the same magnitude as any element in $h_{s r}$ , and any element in $h_{r d}$ has the same magnitude as any element in ${(h}_{r d}$ ), it follows that the ( ${I R S}^{o}$ ) elements all have the same magnitude as the essential IRS model elements. As a consequence of this, $β_{I R S} = β_{s r} β_{r d}$ , and $β_{I R S}^{o} = β_{s r}^{o} β_{r d}^{o}$ .

The higher rate of ( $β_{s d} > β_{s r}$ ) is provided by transmissions supported by the standard model of the IRS, as in [27]. It is contrary to what is in this paper; the highest rate of $β_{s d} > β_{s r}$ is provided by transmissions supported by the optimized model of the IRS.

The difference between $R_{I R S} (N)$ and $R_{S I S O}$ is negligible for most actual values of $N$ when the value is small for $β_{r d}$ , since $\sqrt{β_{s d}} ≫ N α \sqrt{β_{I R S}} = N α \sqrt{β_{s r} β_{r d}}$ . However, the difference in this paper is between $R_{I R S} (N)$ , $R_{S I S O}$ and $R_{{I R S}^{o}}^{o} (N^{o})$ is the smallest since $\sqrt{β_{s d}^{o}} ≫ N^{o} α \sqrt{β_{I R S}^{o}} = N^{o} α \sqrt{β_{s r}^{o} β_{r d}^{o}}$ for most practical values of $N^{o}$ while $β_{r d}^{o}$ is the smallest number for the most practical values of $β_{r d}^{o} < β_{r d}$ . It should be noted that in wireless communications, −50 dB is considered a “large” channel gain. In cases where $β_{s d} \leq β_{s r}$ , an IRS can result in a noticeable performance improvement. Conversely, when $β_{s d}^{o} \leq β_{s r}^{o} < β_{s d}$ , an ( ${I R S}^{o}$ ) can offer a significantly better performance boost.

The coefficient $α$ of the amplitude reflection, the channel gains $β_{s d}, β_{s r}$ , and $β_{r d}$ , and the transmit SNR $p / σ^{2}$ from the right-hand side of (14), where we recall that $β_{I R S} = β_{s r} β_{r d}$ . It is noted that $p \to \infty$ (on the right) is essential $- \sqrt{β_{s d}} / α \sqrt{β_{s r} β_{r d}}$ (on the left). However, the transmitted SNR $p^{o} / σ^{2}$ , the coefficient $α$ of amplitude reflection, and the enhanced channel gains $β_{s d}^{o}, β_{s r}^{o}$ , and $β_{r d}^{o}$ , determine the enhanced value on the right-hand side of (15), where we recall that $β_{I R S}^{o} = β_{s r}^{o} β_{r d}^{o}$ . It noted $- \sqrt{β_{s d}^{o}} / α \sqrt{β_{s r}^{o} β_{r d}^{o}}$ (on the right) gets close to $β_{I R S}^{o} = β_{s r}^{o} β_{r d}^{o}$ (on the left). It means that for each given, $p^{o} \to \infty$ , the most significant rate at a high SNR ( $p / σ^{2}$ ) is achieved by the transmission supported by the IRS for any N. Conversely, the inequality in (14) reduces to (16).

(16)

N > \frac{\sqrt{\frac{1}{(β_{s r} + β_{r d} - β_{s d})}} - \frac{\sqrt{β_{s d}}}{\sqrt{β_{s r} β_{r d}}}}{α}

Also, for any ( $N^{o}$ ), it stands to reason that the transmission with the ( ${I R S}^{o}$ ) will transmit at the most significant rate when the SNR ( $p^{o} / σ^{2}$ ), is high. Conversely, the inequality in (15) simplifies to (17).

(17)

N^{o} > \frac{\sqrt{\frac{1}{(β_{s r}^{o} + β_{r d}^{o} - β_{s d}^{o})}} - \frac{\sqrt{β_{s d}^{o}}}{\sqrt{β_{s r}^{o} β_{r d}^{o}}}}{α}

The numbers $p \to 0$ and $p^{o} \to 0$ have different values, given that $p \to 0$ achieved with $β_{s d} ⩽ β_{s r}$ , while $p^{o} \to 0$ is achieved with ( $β_{s d}^{o} ⩽ β_{s r}^{o} < β_{s d}$ ), it can result in huge numbers. As an illustration, if $α = 1$ , $β_{r d} = - 60 d B$ , $β_{s r} = - 80 d B$ , and $β_{s d} = - 110 dB$ , the result is that (16) becomes $N > 963$ .

Accordingly, the SNR and the number of elements determine whether a standard model for the IRS or an optimized model for the IRS is selected. It assumes throughout this study that both, $β_{I R S}$ and $β_{{I R S}^{o}}^{o}$ are independent of $N$ and $N^{o}$ , respectively.

(18)

N^{o p t (I R S)} = \sqrt[3]{\frac{(2^{R_{d}} - 1) σ^{2}}{α^{2} β_{I R S} P_{e}}} - \frac{1}{α} \sqrt{\frac{β_{s d}}{β_{I R S}}} .

(19)

{N^{o}}^{o p t (I {R S}^{o})} = \sqrt[3]{\frac{(2^{R_{d}} - 1) σ^{2}}{α^{2} β_{{I R S}^{o}}^{o} P_{e}}} - \frac{1}{α} \sqrt{\frac{β_{s d}^{o}}{β_{{I R S}^{o}}^{o}}} .

In most cases, the ideal number of elements in Equations (18) and (19) is not a whole number. Hence, the closest integer, whether greater or smaller, can be used to approximate the true optimum. The SISO situation with N = 0 is the actual ideal value because the best value might potentially be damaging. So, $N^{o p t (S I S O)} = 0$ .

Maximizing energy efficiency while adhering to the data rate ( $R_{d}$ ) limits may be accomplished with the assistance of the SISO, IRS, and ${I R S}^{o}$ , as shown by the findings from [27], where EE of SISO ( ${E E}_{S I S O}$ ), EE of IRS ( ${E E}_{I R S}$ ) and EE of ${I R S}^{o}$ ( ${E E}_{{I R S}^{o}}^{o}$ ) determined by Equations (20)–(22).

(20)

{{E E}_{S I S O} = R_{d} / P}_{S I S O}^{T o t a l}

(21)

{E E}_{I R S} = R_{d} / P_{I R S}^{T o t a l}

(22)

{E E}_{{I R S}^{o}}^{o} = R_{d} / {P^{o}}_{{I R S}^{o}}^{T o t a l}

where (

P_{I R S}^{T o t a l}

), does the IRS use the total power in the system, and (

{P^{o}}_{{I R S}^{o}}^{T o t a l}

), does the IRS consume the total power in the system at the appropriate

R_{d}

. For example,

P_{I R S}^{T o t a l}

consists of the combined hardware dissipation and transmit power. The conventional IIR model’s calculations are given in (23) [27], whereas the optimized IIR model’s calculations are given in (24).

(23)

P_{I R S}^{T o t a l} (N) = \frac{p_{I R S} (N)}{ν} + P_{s} + P_{d} + N P_{e}

(24)

{P^{o}}_{{I R S}^{o}}^{T o t a l} (N^{o}) = \frac{{p^{o}}_{{I R S}^{o}} (N^{o})}{ν} + P_{s} + P_{d} + N^{o} P_{e}

where

p_{I R S} (N)

is the power required for transmission using the IRS as in (27), and

{p^{o}}_{{I R S}^{o}} (N^{o})

is the power required for transmission using the

{I R S}^{o}

model as in (28); furthermore,

P_{s}

and

P_{d}

indicate the hardware dissipated powers at the source and the destination, respectively. Power lost by the element as a result of the phase-shifting circuitry, denoted by

P_{e}

.

v \in [0,1]

where the total power consumption of the SISO system (

P_{S I S O}^{T o t a l}

) determine as in (25), which determines the power amplifier’s efficiency in the SISO situation.

(25)

P_{S I S O}^{T o t a l} = \frac{p_{S I S O}}{ν} + P_{s} + P_{d}

where the power necessary to provide a

R_{d}

, in the SISO case, the standard IRS model and (

{I R S}^{o}

) models are determined by (26), (27), and (28), respectively.

(26)

p_{S I S O} = (2^{R_{d}} - 1) \frac{σ^{2}}{β_{s d}}

(27)

p_{I R S} (N) = (2^{R_{d}} - 1) \frac{σ^{2}}{{(\sqrt{β_{s d}} + N α \sqrt{β_{I R S}})}^{2}}

(28)

{p^{o}}_{{I R S}^{o}} (N^{o}) = (2^{R_{d}} - 1) \frac{σ^{2}}{{(\sqrt{β_{s d}^{o}} + N^{o} α \sqrt{β_{{I R S}^{o}}^{o}})}^{2}}

Suppose the destination demands a particular $R_{d}$ . Then, suppose we use the formulas for the $R_{d} s$ in (11), (12), and (13). In that case, we can determine the transmission power requirements for each of the three possible communication setups.

Consequently, (22) is a non-convex optimization problem for the IRS. Since this optimization problem is non-convex, there is no conventional solution. Consequently, in this paper, we propose a novel artificial intelligence algorithm based on the DS-PSO technique, which will be discussed in the next section.

2.3. The Proposed AI Algorithm to Improve Performance

At (27), the IRS addresses the non-convex optimization problem via an AI algorithm based on the DS-PSO technique. It is a hybrid particle swarm optimization algorithm that integrates both static and dynamic methods. The conventional Particle Swarm Optimization (PSO) methodology employs a search space to commence the particle swarm. To keep an eye on the swarm’s behavior, each particle has a swarm subset, a neighborhood, a speed, and a randomly chosen position. In each iteration, every particle evaluates its current objective function value. Once the fitness of the current solution exceeds that of the particle’s current personal best ( ${P o s}_{b e s t}$ ), the current position is deemed the new personal best ( ${P o s}_{b e s t}$ ). The particle’s position and velocity are updated utilizing Equations (31) and (29) provided below. DS-PSO has a notable similarity to PSO algorithms since it amalgamates the topologies of both static and dynamic iterations of traditional PSO.

The distinguishing feature of DS-PSO is the implementation of two distinct topologies for particles: one for their dynamic neighborhood and another for their static neighborhood. Conversely, the additional dynamic designs prioritize the exploration of the search space over early convergence. A completely random topology is generated concurrently with the execution of the operation. Conversely, alternative dynamic PSO algorithms lose the exploitative characteristics of traditional PSO while employing static topologies.

Swarm particles are modifying their velocities ( $V$ ) and positions ( $P o s$ ) in accordance with Equations (30) and (31), influenced by the neighborhood bests ( $N_{p b e s t}$ ) across all topologies of the DS-PSO.

(29)

\begin{matrix} {V e l}_{p a r} (i) = C_{c} [{V e l}_{p a r} (i - 1) \\ + C_{1} R_{1} ({P o s}_{p a r} (i - 1) - X_{p a r} (i - 1)) \\ + C_{2} R_{2} ({N e i}_{p a r b e s t} (i - 1) - X_{p a r} (i - 1)) \end{matrix}

(30)

\begin{matrix} V_{p a r} (i) = C_{c} [V_{p a r} (i - 1) \\ + C_{1} R_{1} ({P o s}_{p a r} (i - 1) - X_{p a r} (i - 1)) \\ + C_{2} R_{2} (D_{p a r b e s t} (i - 1) - X_{p a r} (i - 1)) \\ + C_{3} R_{3} (S_{p a r b e s t} (i - 1) - X_{p a r} (i - 1))] \end{matrix}

(31)

X_{p a r} (i) = X_{p a r} (i - 1) + V_{p a r} (i)

The velocity is denoted as $V_{p a r} (i)$ in the preceding equations, whereas $X_{p a r} (i)$ , signifies the particle’s (par) position at the current iteration. The particle, individual, dynamic, and static enhanced solutions identified to date in iteration (i) are denoted by ${P o s}_{p a r} (i)$ , $D_{p a r b e s t} (i)$ and $S_{p a r b e s t} (i)$ .

The DS-PSO algorithm’s main new idea, and what makes it different from other optimization methods like standard PSO or Genetic Algorithms (GA), is its hybrid topology. In traditional PSO, there is only one social network (like a global best). This can cause problems to converge too quickly when they are complex and have more than one mode, like IRS phase-shift optimization. DS-PSO, on the other hand, keeps two separate social networks for each particle at the same time: a stable static topology ( $S_{p a r b e s t}$ ) that preserves reliable social information and promotes consistent exploitation, and a randomly changing dynamic topology ( $D_{p a r b e s t}$ ) that injects novelty into the search process, preventing stagnation in local optima. This hybrid approach is designed to strike the ideal balance between exploitation (improving known good solutions) and exploration (searching for new areas of the solution space). Unlike other algorithms, DS-PSO adapts its search strategy naturally, making it ideal for the high-dimensional, non-convex optimization problem presented by IRS, where determining the optimal phase-shift configuration is crucial to achieving maximum energy efficiency.

The hybrid nature of DS-PSO, combining both static $S_{p a r b e s t} (i)$ and dynamic $D_{p a r b e s t} (i)$ Social topologies are its key adaptive strength. A major issue with metaheuristics is directly addressed by this design: striking a balance between exploration (finding new areas) and exploitation (improving areas that are already good).

Purely static topologies, such as ring structures, facilitate stable convergence, making them ideal for exploitation. However, it could cause convergence to a local optimum too quickly in challenging, multi-modal problems like IRS phase-shift optimization. Conversely, a purely dynamic topology is highly exploratory but may be aimless, which causes instability and slow convergence.

By not requiring you to select between these two plans, DS-PSO transforms the situation. By providing a consistent, long-range source of social information, the static topology helps people stay on course and prevents them from acting irrationally. In contrast, the dynamic topology adds interest and randomness to the search process. By allowing particles to receive assistance from various randomly assigned neighbors, this aids them in leaving local optima. The algorithm’s behavior is determined by the acceleration coefficients ( $C_{1}$ , $C_{2}$ and $C_{3}$ ). In situations where the fitness landscape is simpler and convex, the static component ( $C_{3}$ ) will provide consistent guidance, which will lead to fast and stable convergence. In very complicated, non-convex situations like our IRS optimization problem, the dynamic component ( $C_{2}$ )’s ability to explore becomes even more important. This lets the swarm find better phase-shift configurations that a purely static approach might miss.

To keep speeds from getting too fast, the constriction coefficient, ( $C_{c}$ ), is usually set at about 0.7298438. In Equation (29), the acceleration coefficients ( $C_{1}$ ) and ( $C_{2}$ ) make particles more likely to be drawn to ${P o s}_{p a r}$ and $N_{p a r b e s t}$ , respectively. The total acceleration coefficient for standard PSO is 4.1, and the individual coefficients ( $C_{1}$ ) and ( $C_{2}$ ) are both 2.05. Also, the acceleration coefficients ( $C_{1}$ , $C_{2}$ and $C_{3}$ ) are used in Equation (30) to make particles more attracted to ${P o s}_{p a r} (i)$ , $D_{p a r b e s t} (i)$ and $S_{p a r b e s t} (i)$ , respectively. Each particle will attain optimal static, dynamic, and individual performance. Because of this, DS-PSO finds three acceleration coefficients instead of the two that the traditional PSO algorithm finds. The acceleration coefficients ( $C_{1}$ , $C_{2}$ and $C_{3}$ ) each give a value of 1.366666667, and they are set at 4.1/3.

To make research easier, the components of the velocity equation are multiplied by a vector of random values, $R_{1}$ , $R_{2}$ , and $R_{3}$ , that are limited to the range [0,1]. The search space is defined by the interval [ $V_{m i n}$ ; $V_{m a x}$ ], which shows the minimum and maximum values of the search space. Each element of $V_{p a r}$ must be within this range. The particle exhibits a preference for $D_{p a r b e s t}$ and $S_{p a r b e s t}$ , over $N_{p a r b e s t}$ , the optimal neighbors. Therefore, while evaluating the static and dynamic topologies of particles, this is the ideal solution [35,36,37].

The pseudocode flow of the sequence of operations of the DS-PSO algorithm is shown in [37] as a reference for implementation details.

Below is a pseudocode that visually represents the dual influence of static and dynamic topologies in DS-PSO. This format is designed to provide a step-by-step guide to the operation of the DS-PSO algorithm. The pseudocode has been streamlined to focus on explaining the intuition behind the hybrid topology and the key equations for IRS Phase-Shift Optimization, illustrating the process flow. The parameters used in simulating the algorithm are as shown in Table 1.

Table 1:

The main parameters used in the DS-PSO algorithm.

Parameter	Value
Iteration ( $i$ )	1000
Particles (par)	10
coefficients of acceleration ( $C_{1}$ = $C_{2}$ = $C_{3}$ )	4.1/3
The minimum probability of restructuring neighborhoods	0.1
The maximum probability of restructuring neighborhoods	0.2
Intervals for the probability of restructuring neighborhoods	0.5
Intertie coefficient (spaced frequency points)	1
The search space’s minimum values ( $V_{m i n}$ )	1
Maximum values in the search space ( $V_{m a x}$ )	70

DS-PSO Algorithm: Structured Pseudocode

Algorithm: DS-PSO for IRS Phase-Shift Optimization

Inputs:

par: Number of particles in the swarm
f: Objective function (e.g., to maximize Energy Efficiency, EE)
${m a x}_{I t e r}$ : Maximum number of iterations
$P_{r e s t r u c t u r e}$ : Probability of restructuring dynamic neighborhoods
$V_{m i n}$ ; $V_{m a x}$ : Minimum and maximum velocity in the search space

Outputs:

$S_{p a r b e s t}$ : Global best position found (optimal phase-shift configuration)
f( $S_{p a r b e s t}$ ): Best objective function value (maximized EE)

Initialization:

For each particle $i$ = 1 to par:

Initialize position $X_{p a r} (i)$ randomly within the search space [ $V_{m i n}$ ; $V_{m a x}$ ].
Initialize velocity $V_{p a r} (i)$ = 0.
Initialize personal best position;

{P o s}_{p a r} (i) = X_{p a r} (i) .

Evaluate personal best fitness f( ${P o s}_{p a r} (i)$ ).

2.
Initialize static topology (e.g., Ring) for all particles to define $S_{p a r b e s t} (i)$ .
3.
Initialize the dynamic topology by randomly assigning $D_{p a r b e s t} (i)$ , for each particle.
4.
Initialize global best $S_{p a r b e s t}$ .

Main Loop:

for iteration = 1 to ${m a x}_{I t e r}$ do
for each particle $i$ do
Evaluate the fitness f( $X_{p a r} (i)$ )
if f( $X_{p a r} (i)$ ) is better than f( ${P o s}_{p a r} (i)$ ) then
Update personal best: ${P o s}_{p a r} (i)$ = $X_{p a r} (i)$
end if
Identify the static neighborhood best $S_{p a r b e s t} (i)$ , from the static topology.
Identify the dynamic neighborhood best $D_{p a r b e s t} (i)$ , from the dynamic topology.
Update Velocity using Equation (30):
Bound $V_{p a r} (i)$ within [ $V_{m i n}$ ; $V_{m a x}$ ].
Update Position using Equation (31):
Bound $X_{p a r} (i)$ , within the search space.
end for (particle loop)
if $r a n d ()$ < $P_{r e s t r u c t u r e}$ then
Restructure all dynamic topologies (randomly reassign $D_{p a r b e s t}$ for each particle.)
end if
Update the global best solution $S_{p a r b e s t}$
end for (iteration loop)

Return

S_{p a r b e s t}

, f(

S_{p a r b e s t}

)

Traditional PSO employs a single social topology (e.g., a global best) to guide the swarm; this can lead to premature convergence in complex problems, such as IRS phase-shift optimization, where the search space is highly multimodal. The DS-PSO algorithm hybridizes this approach by maintaining two distinct social networks for each particle: a static topology (e.g., a ring or star structure) that preserves stable, long-range social information and promotes exploration, and a dynamic topology that randomly changes neighbors over iterations, preventing premature stagnation.

In the context of optimizing an IRS with N elements, each particle’s position represents a candidate set of phase shifts (θ₁, θ₂, ..., θ_N). A traditional PSO might become trapped in a local optimum, failing to find the optimal phase configuration that maximizes the SNR at the destination. On the other hand, the dynamic part of DS-PSO lets a particle get help from a random, different part of the swarm from time to time, which lets it "jump" out of a local valley. The static part makes sure that it still follows a stable path from its stable neighbors. This hybrid strategy works especially well for IRS optimization because it strikes a good balance between the need to thoroughly search the large phase-shift space (exploration) and the need to improve and focus on the best solution found (exploitation).

3. Results

This section shows the results of the simulation and a comparison of the proposed AI-optimized IRS model’s performance against benchmark systems. It looks at important metrics like energy efficiency and data rate in different operational modes.

This section assesses the appropriateness of approximate outcomes to determine the selection between a standard IRS model and an ( ${I R S}^{o}$ ) model. It determines whether the experimental setups employed in Section 2 function in the high or low SNR regime. A numerical analysis of the systems will be conducted. Subsequently, the EE of the transmission aided by the model of ( ${I R S}^{o}$ ) is computed using the mathematical equations mentioned in Section 2 of this paper. A comparative analysis is then conducted with the findings of previous research studies.

3.1. Transmit Destination

The 3GPP Urban Micro (UMi) model, as described in reference [38]. The carrier frequency is set at 3 GHz to depict the channel gains accurately. The line-of-sight (LOS) and non-line-of-sight (NLOS) Urban Microcell (UMi) models, specified for distances of 10 m or greater, are employed. Let us say that the antenna gains for the transmitter and receiver, measured in dBi, are $G_{t}$ and $G_{r}$ , respectively. It is possible to use UMi at both LOS and NLOS distances.

For the simulations in this study, we assume that the transmitter and receiver antennas ( $G_{t}$ and $G_{r}$ ) located between the source and the IRS have equal gains of 5 decibels of isotropic radiated power (dBi) within a distance of 100 m while disregarding shadow fading. Upon reaching the desired destination, the individual possesses a telephone with an omnidirectional antenna with a gain of 0 dBi.

The transmission in wireless communication networks is influenced by factors such as channel gain and distance. We made a detailed channel gain and distance diagram to study and model a wireless communication system that uses an IRS. This diagram is shown in Figure 2 for the wireless communication system supported by the IRS. The communication system model proposed in this study closely resembles the configuration depicted in Figure 2. However, it utilizes the improved IRS model instead of the standard IRS model and adopts the improved LOS. Figure 2 depicts the stationary positions of both the source and the IRS or ( ${I R S}^{o}$ ) proposed in this study. The simulations for this study assume the distances between the source and the standard IRS or ${I R S}^{o}$ , as depicted in Figure 2, respectively. The proposed distance between the source and the IRS d₁ is 70 m. The user/destination can be located within the range of the source as long as the distance between them (d₂) is greater than or equal to 10.

Figure 2: Destination variables (d1) and (d2) for the simulation setup of the standard IRS model. — **Figure 2:** Destination variables (d₁) and (d₂) for the simulation setup of the standard IRS model.

Figure 2 illustrates the support of the IRS in facilitating transmission within the wireless communication system by generating line-of-sight (LOS) channels. A standard LOS version generates two distinct line-of-sight (LOS) channels. The LOS between the source and the IRS is denoted as $β_{s d}$ , while the LOS between the IRS and the user or destination is denoted as $β_{r d}$ . Conversely, the NLOS version between the source and the user or destination generates a channel denoted as $β_{s d}$ . The Equation $β_{I R S} = β_{s r} β_{r d}$ is used to represent the relationship between $β_{I R S}$ , $β_{s d}$ , and $β_{r d}$ .

In the NLOS case, the weak channel gain between the source and the user (or destination) means that an Intelligent Reflecting Surface (IRS) needs to be used to improve signal transmission in next-generation wireless communication networks. The IRS makes LOS channels that work better than NLOS channels. Also, as the distances get longer, the channel gain values with LOS go down, but they are still better than those with NLOS. This is why LOS properties were used in the design of a wireless communication system that was made easier by using an IRS, which had a lot of benefits.

As a result, using IRS in wireless communication networks has created two LOS channels. There is one channel that goes from the source to the IRS. On the other hand, the link between the IRS and the user or destination makes these networks work better when sending data.

The LOS channels within the model of ( ${I R S}^{o}$ ) will consist of two channels. The initial channel connecting the source and the model of ${I R S}^{o}$ is denoted as $β_{s r}$ . This channel’s channel is optimized by maximizing the LOS between the source and the ( ${I R S}^{o}$ ), denoted as $β_{s r}$ . The second channel between the ( ${I R S}^{o}$ ) and the user or destination is created by optimizing the LOS channel between the ( ${I R S}^{o}$ ) and the user or destination, denoted as $β_{r d}$ . The Equation can be simplified as $β_{{I R S}^{o}}^{o}$ = $β_{s r}^{o}$ and $β_{r d}^{o}$ .

The initial step in the simulation involves calculating the channel gain value ( $β_{s d}$ ) for the SISO case in the communication system depicted in Figure 2. This calculation uses Equation (32) due to its NLOS nature. The channel gains values ( $β_{r d}$ and $β_{s r}$ ) with the standard IRS of the communication system in Figure 2 can be calculated using Equation (32). These values are determined based on the distance d1 and the antenna gains ( $G_{t}$ , and $G_{r}$ ), between the source and the IRS; this is to determine the values of $β_{s d}$ and $β_{s r}$ . Furthermore, the channel gain values ( $β_{s r}^{o}$ and $β_{r d}^{o}$ ) are calculated using Equation (33) for the proposed ( ${I R S}^{o}$ ) model for the communication system. The channel gain using the improved IRS is the improved LOS version.

(32)

β (d) [d B] = G_{t} + G_{r} + \{\begin{array}{l} - 37.5 - 22 \log_{10} (\frac{d}{1 m}) & i f L O S \\ - 35.1 - 36.7 \log_{10} (\frac{d}{1 m}) & i f N L O S \end{array}

(33)

β^{o} (d) [d B] = O p t i m i z e d [G_{t} + G_{r} + {- 37.5 - 22 \log_{10} (\frac{d}{1 m})}] i f O p t i m i z e d L O S

Given the superior performance of the optimized LOS configuration relative to the standard LOS version, it is reasonable to expect that the proposed IRS model in this study will achieve improved performance compared to the conventional IRS model. Thus, this study’s proposed ( ${I R S}^{o}$ ) can enhance the performance of 6G communication systems. This claim can be supported in this paper by using an IRS system performance evaluation measure. Therefore, this paper suggests implementing (energy efficiency compared to data rate) evaluation measures for IRS systems, specifically focusing on the standard IRS model and the proposed ( ${I R S}^{o}$ ) model that is optimized in this paper. A comparative analysis is then performed to compare the findings of this research with previous studies on (energy efficiency compared to data rate) in alternative IRS models.

3.2. Energy Efficiency Compared to Data Rate

The simulation involves evaluating the performance of the SISO case, the standard IRS model, and the proposed ( ${I R S}^{o}$ ) model based on their energy efficiency. In this paper, we determined the parameters associated with energy efficiency, including the quantity of the data rate, which is attributed to the significance of these parameters in enhancing the performance of the IRS. In this section, we aim to calculate energy efficiency values using the parameters from Table 2.

Table 2:

The parameters for the simulation in this paper.

Parameter	Value
Bandwidth (B)	10 MHz
Carrier frequency (FC)	3 GHz
Noise figure	10 dB
Noise power	$- 94 d B m$
Power spectral density of noise	−174 dBm/Hz
$α$	1
Range of data rate ( $R_{d}$ )	[0 10]
The source’s transceiver hardware power dissipation ( $P_{s}$ )	100 mW
Dissipation of power in the destination’s transceiver hardware ( $P_{d}$ )	100 mW
The dissipation of power per IRS element (mw) ( $P_{e}$ )	5 mW
Power amplifier efficiency at the source ( $v$ )	0.5
Range of distance ( $d$ )	70 m
Distance ( $d_{1}$ ) between the source and IRS/ ${I R S}^{o}$	70 m
The minimum distance ( $d_{2}$ ), between the source and destination	10 m

In the simulations presented in this paper, we will utilize the proposed algorithm, in addition to the LOS version discussed in Section 3.1, which has been improved.

Simulations were performed for the SISO case, the standard IRS model, and the proposed IRS model that is optimized in this study. The simulations compared energy efficiency in terms of data rate. Next, the findings of this study will be compared to previous research on energy efficiency, particularly in terms of data.

Calculating energy efficiency requires determining the total transmission power, which in turn requires calculating the needed transmission capacity and the number of elements within the IRS. Calculating the number of elements needed in the IRS involves determining its channel gain values, which provide an estimate of the overall channel performance. ( $β_{r d}$ and β_sr) related to the IRS are essential in determining the number of reflective elements within the IRS. Therefore, we sought to use improved channel gain values. The proposed algorithm relates ( $β_{s r}^{o} {a n d β}_{r d}^{o}$ ) to the ( ${I R S}^{o}$ ) proposed in this paper.

To obtain the results of this study, the energy efficiency values for the SISO case, the standard IRS, and the ( ${I R S}^{o}$ ) proposed in this paper are calculated using Equations (20)–(22), respectively. Equations (23)–(25) are used to find the total transmission power values for the SISO cases, the standard IRS, and the ( ${I R S}^{o}$ ) proposed in this paper. Equations (26)–(28) are used to figure out how much power each SISO case needs, including the standard IRS and the ( ${I R S}^{o}$ ) proposed in this paper. Equations (18) and (19) can be used to figure out how many reflective elements are in both the standard IRS and the proposed ( ${I R S}^{o}$ ) model. It’s important to note that there are no reflective elements in the SISO case. The channel gains ( $β_{r d}$ and β_sr) with the standard IRS of the communication system depicted in were determined using Equation (32). The channel gains values ( $β_{s r}^{o}$ and $β_{r d}^{o}$ ) with the ( ${I R S}^{o}$ ). The performance of the communication system was determined using Equation (33). The channel gain values obtained from Equations (32) and (33) are included in Equations (18) and (19), respectively.

This study conducted simulations to evaluate the energy efficiency values for three cases: SISO, IRS standards, and ( ${I R S}^{o}$ ) proposed in this paper. As such, the simulations in Section 3.2 of this study were formulated to evaluate energy efficiency in relation to data rate.

This study conducts a comparative analysis of energy efficiency values in relation to data rates. Based on the simulations performed in this study, the energy efficiency values concerning data rates for the SISO case, standard IRS, and ( ${I R S}^{o}$ ) proposed in this paper are shown in Table 3 and Figure 3 and Figure 4.

Table 3:

The comparison between energy efficiency values concerning data rate values.

$Range No . of R_{d}$	Range 1	Range 2	Range 3	Range 4
Sample No. of $R_{d}$	Sample 1	Sample 2	Sample 3	Sample 4	Sample 5	Sample 6	Sample 7
Data rate $R_{d}$	0.01	2	4	5	6	8	10
EE with SISO	0.366	93.02	146.4	142.1	116.5	54.22	18.81
EE with IRS	0.366	93.02	146.4	142.1	139.2	122.2	99.19
EE with Optimized IRS ( ${I R S}^{o}$ )	0.366	73.21	146.4	183	219.6	292.8	366

Figure 3: Energy efficiency compared to the data rate (

R

d

) function. — **Figure 3:** Energy efficiency compared to the data rate ( $R_{d}$ ) function.

Figure 4: Energy efficiency values compared to data rate values. — **Figure 4:** Energy efficiency values compared to data rate values.

Table 3 and Figure 4 reveal that the proposed ( ${I R S}^{o}$ ) model underperforms the SISO and standard IRS models at very low data rates (e.g., $R_{d}$ = 0.01- and 2-bit/s/Hz); this is not an artifact of the optimization algorithm but a fundamental system trade-off. At minimal data rates, the required transmit power is very low. The static hardware power dominates the total power consumption in an IRS-assisted system ( $P_{s}$ , $P_{d}$ ) and the power dissipated by the IRS elements ( $N P_{e}$ ), as defined in Equations (23) and (24). The energy efficiency (EE) metric, defined as bits transmitted per Joule, is thus low because the denominator (total power) is significant even though the numerator (data rate) is small. A SISO system, with zero IRS elements (N = 0), has a lower total power overhead at these low rates and thus achieves a comparable or slightly higher energy efficiency (EE). The DS-PSO algorithm correctly optimizes for this regime by effectively ‘turning off’ the IRS benefit when it is not needed. The superior performance of models like PSO-IRS and GA-IRS [32] at $R_{d}$ = 0.01 is likely due to a different system model or cost function that does not penalize the IRS’s hardware power consumption as heavily.

The model of ( ${I R S}^{o}$ ) achieves increasing energy efficiency (EE) with increasing data rate. In contrast, SISO and standard IRS models degrade after reaching a peak, as shown in Figure 3.

Figure 3 shows the energy efficiency values, ranging from 0 to 400 Mbit/Joule, and the data rate values, ranging from 0 to 10-bit/s/Hz. These values were observed for the SISO case and the standard and ( ${I R S}^{o}$ ) models proposed in this study. The energy efficiency index of the proposed ( ${I R S}^{o}$ ) consistently increased as the data ratio increased. In contrast, the indicators for the standard IRS model and the SISO status decreased as the data ratio increased. Figure 4 was created to analyze the data in Figure 3 based on three cases: the SISO case, the standard IRS model, and the proposed ( ${I R S}^{o}$ ) model.

There are sampled data points from Figure 3, highlighting the ${I R S}^{o}$ ’s superior performance at data rates > 4-bit/s/Hz and its lower performance at very low rates due to hardware power overhead, as shown in Figure 4.

Figure 4 shows the sampling of energy efficiency indicators in three cases: the SISO case, the standard IRS model, and the proposed ( ${I R S}^{o}$ ) model. The purpose is to determine the energy efficiency values and data rate accurately. Seven samples were collected at (0.1, 2, 4, 5, 6, 8, and 10) bit/s/Hz of data rate. The performance trade-off and the superior high-rate performance of the ( ${I R S}^{o}$ ) model, as demonstrated in Table 3.

Table 3 was created based on the energy efficiency values and the proportion of data obtained from the energy efficiency indicators in Figure 4. Table 3 compares energy efficiency values for three cases: the SISO case, the standard IRS model, and the proposed ( ${I R S}^{o}$ ) model. The comparison is conducted using specific data, with energy efficiency measured in Mbit/Joule and data rate measured in bits per second per hertz.

To make it easier to analyze, it was important to split the data into five separate ranges, based on the data in Figure 4 and Table 3. The data rate can be split into five ranges: the initial range has a data rate of 0.0; the second range has a data rate between 0.01 bit/s/Hz and 4 bit/s/Hz; the third range has a data rate of 4 bit/s/Hz; the fourth range has a data rate between 4 bit/s/Hz and 5 bit/s/Hz; and the final range has a data rate greater than 4 bit/s/Hz but less than or equal to 5 bit/s/Hz. Two ranges with equal energy efficiency values are observed in all three cases: the SISO case, the standard IRS model, and the proposed ( ${I R S}^{o}$ ) model. These ranges, namely the first and third ranges, have distinct energy efficiency values from each other. The energy efficiency value is 0.366 Mbit/Joule with a data rate of 0.01-bit/s/Hz and increases to 146.4 Mbit/Joule with a data rate of 4-bit/s/Hz.

In the second range, where the data rate ranges from 0.01-bit/s/Hz and 4-bit/s/Hz, the energy efficiency values for the SISO case and the standard IRS model without the proposed ( ${I R S}^{o}$ ) model are the same. The energy efficiency values range from 0.366 Mbit/Joule to 146.4 Mbit/Joule, based on the data rate. When a sample was taken from the second range at a data rate of 2-bit/s/Hz, it was found that the proposed ( ${I R S}^{o}$ ) model was less energy efficient than both the SISO case and the standard IRS model. Consequently, the results of this study demonstrate that the proposed ( ${I R S}^{o}$ ) model displays low energy efficiency at reduced data rates.

The energy efficiency values are identical for both the SISO case and the standard IRS model without the proposed ( ${I R S}^{o}$ ) model in the fifth range (data rate > 4-bit/s/Hz and ≤ 5-bit/s/Hz). So, the energy efficiency value is between 142.1 Mbit/Joule and 146.4 Mbit/Joule, depending on the exact data rate values. When a sample was taken from the fifth range with a data rate of 5-bit/s/Hz, it was found that the proposed ( ${I R S}^{o}$ ) model’s energy efficiency is 183 Mbit/Joule. This value surpasses the energy efficiency observed in the SISO case and the standard IRS model. The results suggest that this study’s proposed ( ${I R S}^{o}$ ) model achieves high energy efficiency with a high data rate.

In the fourth range, where the data rate is higher than 4 bits/s/Hz, the energy efficiency values are different for the three cases: the SISO case, the standard IRS model, and the proposed IRS model that this study optimized. Taking four samples from the fourth range of the data rate (5, 6, 8, and 10-bit/s/Hz) shows that the energy efficiency goes down for both the SISO case and the standard IRS models as the data rate goes up. Conversely, it is observed that the proposed ( ${I R S}^{o}$ ) system demonstrates an upward trend in energy efficiency as the data rate increases. Accordingly, the energy efficiency limit was highest among the SISO case, the standard IRS model, and the proposed ( ${I R S}^{o}$ ) model, based on the samples in the fourth range, at a data rate of 10-bit/s/Hz. The energy efficiency results for different cases at a data rate of 10-bit/s/Hz were as follows: 18.81 Mbit/Joule for SISO, 99.19 Mbit/Joule for the standard IRS model, and 366 Mbit/Joule for the proposed ( ${I R S}^{o}$ ) model.

If the data rate exceeds 4-bit/s/Hz, the energy efficiency of this study’s proposed ( ${I R S}^{o}$ ) is higher than the energy efficiency of the SISO case and the standard IRS model. The findings of this study suggest that the proposed ( ${I R S}^{o}$ ) has superior energy efficiency at higher data rates.

To facilitate the analysis of the data presented in Table 4, we designed Figure 5 to improve data interpretation. Table 4 shows an analytical comparison of energy efficiency versus data rate for the SISO systems and different IRS models, which are the standard model, the improved model in this study, models improved by the PSO algorithm, and single, dual, and triple IRS models in [39], and the Genetic algorithm (GA) in [40]. This analysis assesses the efficacy of SISO, standard IRS, and ${I R S}^{o}$ models relative to prior research, emphasizing the tradeoff between data rate ( $R_{d}$ ) and energy efficiency. Table 4 shows how IRS optimization techniques affect the results and gives us an idea of how well multi-IRS setups can grow.

Table 4:

Energy Efficiency (EE) vs. Data Rate ( $R_{d}$ ) for SISO, standard IRS, optimized IRS ( ${I R S}^{o}$ ) model in this study, and IRS models in previous studies.

$Data Rate (R_{d}$ ) [bit/s/Hz]	EE with SISO [Mbit/Joule] [in This Study]	EE with Standard IRS [Mbit/Joule] [in This Study]	EE with Single-IRS [Mbit/Joule] [39]	EE with Double-IRS [Mbit/Joule] [39]	EE with Triple-IRS [Mbit/Joule] [39]	EE with PSO-IRS [Mbit/Joule] [40]	EE with GA-IRS [Mbit/Joule] [40]	EE with Optimized IRS [Mbit/Joule] [in This Study]
0.01	0.366	0.366	0.366	0.366	0.366	44	44	0.366
2	93.02	93.02	20	34	50	42	42	73.21
4	146.4	146.4	40	68	100	EE < 25	EE < 25	146.4
5	142.1	142.1	50	85	125	EE < 15	EE < 15	183
6	116.5	139.2	60	102	150	EE < 10	EE < 10	219.6
8	54.22	122.2	80	136	200	EE < 5	EE < 5	292.8
10	18.81	99.19	100	170	250	0.5	0.5	366

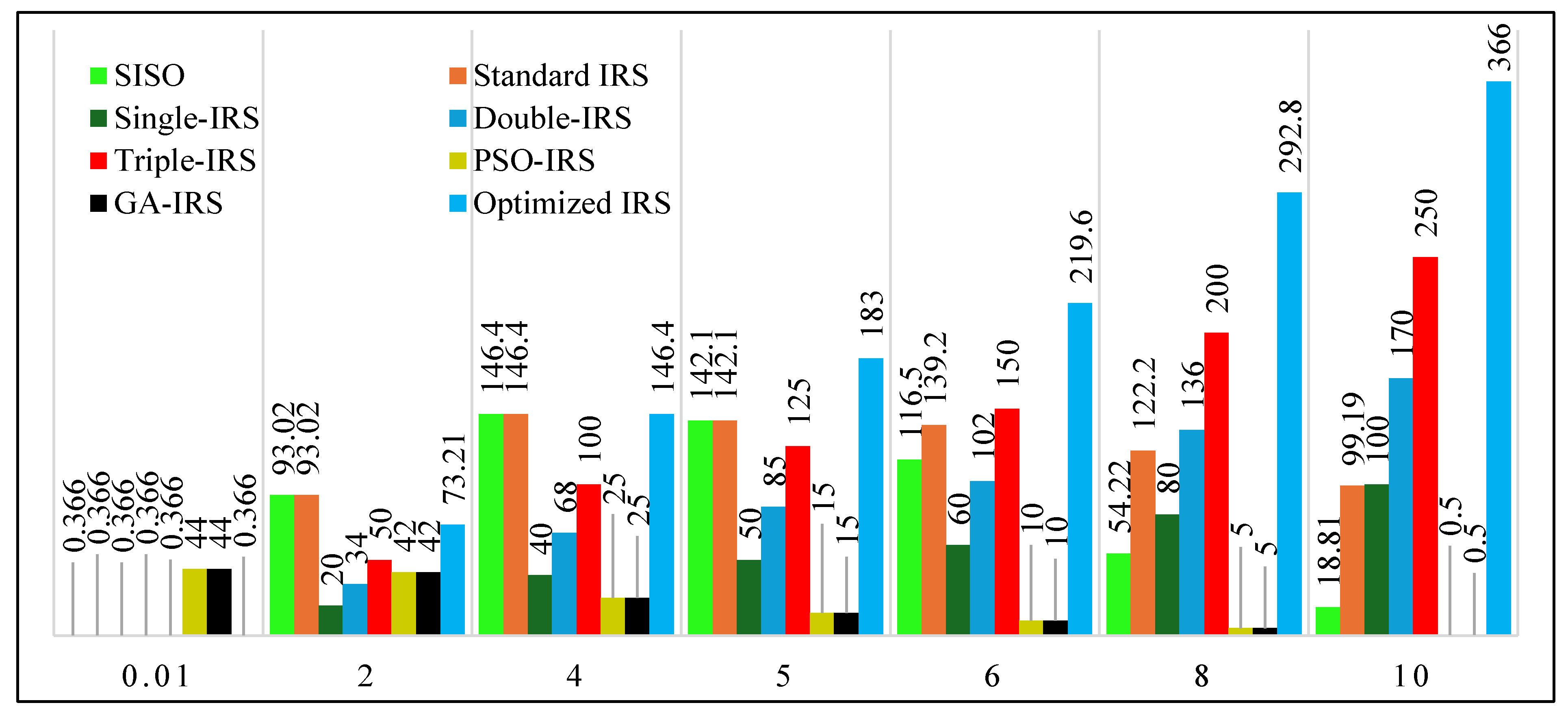
Figure 5: Energy efficiency compared to the data rate for (SISO, Standard IRS, Optimized IRS (

I
R
S

o

) model in this study and IRS models in previous studies. — **Figure 5:** Energy efficiency compared to the data rate for (SISO, Standard IRS, Optimized IRS ( ${I R S}^{o}$ ) model in this study and IRS models in previous studies.

Low Data Rate Regime ( $R_{d}$ ≤ 0.01 bit/s/Hz): At extremely low data rates, all models (SISO, standard IRS, proposed ${I R S}^{o}$ , IRS models improved by the PSO algorithm and the GA algorithm in [40], and single, dual, and triple IRS models in [39].) exhibit identical EE (~0.366 Mbit/Joule); this suggests that IRS deployment does not provide significant gains when the system operates at minimal throughput, likely due to negligible beamforming benefits at such low rates.

Moderate Data Rate (2 ≤ $R_{d}$ ≤ 6-bit/s/Hz): The standard IRS matches SISO performance up to $R_{d}$ = 4-bit/s/Hz, indicating no substantial improvement without optimization. The proposed ${I R S}^{o}$ begins outperforming both SISO and standard IRS at $R_{d}$ = 5-bit/s/Hz, achieving 183 Mbit/Joule compared to 142.1 Mbit/Joule for SISO. (Single/Double/Triple-IRS [39]) shows a linear increase in EE with $R_{d}$ , but even the Triple-IRS (150 Mbit/Joule at $R_{d}$ = 6) underperforms compared to the proposed ${I R S}^{o}$ (219.6 Mbit/Joule). (IRS with PSO/GA, or PSO-IRS and GA-IRS [40]) shows high EE at very low $R_{d}$ (44 Mbit/Joule at $R_{d}$ = 0.01) but quickly degrades beyond $R_{d}$ = 2, suggesting inefficiency in handling higher data rates.

High Data Rate ( $R_{d}$ ≥ 8-bit/s/Hz): The proposed ${I R S}^{o}$ demonstrates superior scalability, reaching 292.8 Mbit/Joule at $R_{d}$ = 8 and 366 Mbit/Joule at $R_{d}$ = 10, far exceeding all other models. The standard IRS shows moderate improvements over SISO, but remains significantly below the proposed ( ${I R S}^{o}$ ). The Triple-IRS model reported in [39] achieves a peak energy efficiency of 250 Mbit/Joule at $R_{d}$ = 10, which remains 32% lower than that of the (IRS⁰) model. The PSO-IRS and GA-IRS models discussed in [40] do not maintain competitive energy efficiency for $R_{d}$ = 4, demonstrating their inadequacies in high-throughput contexts.

To measure how much better the ( ${I R S}^{o}$ ) model is than other methods, we use Table 4 to find the percentage increase in Energy Efficiency (EE) at different data rates. Here is a summary of the results:

${I R S}^{o}$ vs. SISO: At $R_{d}$ = 2, ${I R S}^{o}$ does worse than SISO, but at higher data rates (up to 1846% at $R_{d}$ = 10), it does much better. This means that IRS optimization works best in situations where a lot of data is being sent.

The ${I R S}^{o}$ is the same as the standard IRS at low $R_{d}$ . Still, it gives big gains (up to 269%) at higher rates, which shows that optimization algorithms make IRS more efficient as data needs grow.

${I R S}^{o}$ vs. (Single/Double/Triple-IRS [39]): The ${I R S}^{o}$ consistently outperforms [39]’s models by 46.4–266%. A single ${I R S}^{o}$ is 46.4% better than a Triple-IRS, which shows that optimization is more effective than adding more IRS layers.

When comparing ${I R S}^{o}$ to PSO-IRS and GA-IRS [40], the PSO-IRS and GA-IRS models work very well at very low $R_{d}$ (0.01), but they fail at higher data rates. The ${I R S}^{o}$ dominates beyond $R_{d}$ = 2, with >485% improvement at $R_{d}$ = 4.

This analysis and comparison in Table 5 make it easy to see how much better the proposed ( ${I R S}^{o}$ ) model is than earlier studies, showing how useful it could be for future 6G communication systems.

Table 5:

Overall superiority summary percentage improvement of optimized IRS ( ${I R S}^{o}$ ) in this study over other models.

Comparison	Best Improvement (%)	Worst Case (%)
Optimized IRS ( ${I R S}^{o}$ ) in this study vs. SISO in this study	+1846% ( $R_{d}$ = 10)	−21.3% ( $R_{d}$ = 2)
Optimized IRS ( ${I R S}^{o}$ ) in this study vs. Standard IRS in this study	+269% ( $R_{d}$ = 10)	−21.3% ( $R_{d}$ = 2)
Optimized IRS ( ${I R S}^{o}$ ) in this study vs. (Single-IRS [39])	+266% (all $R_{d}$ ≥ 2)	–
Optimized IRS ( ${I R S}^{o}$ ) in this study vs. (Triple-IRS [39])	+46.4% (all $R_{d}$ ≥ 2)	–
Optimized IRS ( ${I R S}^{o}$ ) in this study vs. (PSO-IRS and GA-IRS [40])	>+485% ( $R_{d}$ = 4)	−99.2% ( $R_{d}$ = 0.01)

When comparing the proposed ( ${I R S}^{o}$ ) model to existing models from previous studies in terms of energy efficiency and data rate, it is clear that the ( ${I R S}^{o}$ ) model is better than the others. It keeps high energy efficiency in both sending and receiving data, even at high data rates. It is also the best model for improving transmission performance in sixth-generation communication networks. But it can still send data at a high rate of at least 10 Mbps while using energy efficiently at a rate of at least 366 Mbit/Joule. Consequently, we advocate for the implementation of the proposed methodology and ( ${I R S}^{o}$ ) model in this study to improve transmission performance in 6G networks with the assistance of the IRS.

The simulation results in this study utilize the 3GPP Urban Micro (UMi) channel model, providing a standardized and theoretically robust framework for comparative analysis. However, it is important to remember that the proposed model is useful, but it makes some simplifications and may not fully capture the complexities of real-world radio propagation environments, such as spatial correlations, severe scattering, and changing interference patterns. Therefore, future research must prioritize validation in more intricate and realistic scenarios in order to further strengthen the practical relevance of our findings.

4. Discussion

In order to contextualize the simulation results within actual 6G deployment scenarios, this section addresses the practical implementation challenges and limitations of the proposed AI-optimized IRS model, such as channel estimation, hardware imperfections, and scalability.

4.1. Channel Model Assumptions and Dynamic Environments

For the sake of tractability, our analysis uses deterministic flat-fading channels to obtain closed-form expressions for data rate and energy efficiency, which is a common strategy in the foundational IRS literature [19,21]. We acknowledge that time-varying fading, shadowing, and blockages are characteristics of real-world environments. Accurate Channel State Information (CSI), which is essential to an IRS’s operation, is difficult to obtain in situations involving mobile users that are changing quickly. Channel estimation is made more difficult by IRS elements’ passive nature, which prevents them from sending or receiving pilot signals [16, 23]. To assess the robustness of the DS-PSO algorithm in uncertain environments, future studies must incorporate stochastic channel models (like Rayleigh or Rician fading) and sophisticated channel estimation techniques. The dynamic topology part of the algorithm, designed for exploration, may be very helpful in adapting to changing environments.

Channel Estimation Overhead: It is very difficult to obtain the CSI for the IRS-destination and source-IRS links, particularly when there are many Nᵒ elements. The costs of this estimate must be included in a complete system model.

Dynamic Settings: The proposed model operates on static channels. Since moving objects, such as cars and people, can alter channel conditions rapidly, robust and low-latency optimization algorithms are required to adapt to these changes.

4.2. Hardware Imperfections

Perfect IRS elements with continuous phase shifts and perfect reflection efficiency (α = 1) are assumed in our model. Hardware is not perfect in real life. Phase shifters frequently undergo quantization (e.g., 1–2 bits), which leads to quantization errors that reduce the beamforming gain. Furthermore, the overall performance of the system may be impacted by amplitude variations, mutual coupling between adjacent elements, and the phase-shifting circuitry’s non-linear power consumption ( $P_{e}$ ). In these less-than-ideal circumstances, the reported energy efficiency gains would need to be reassessed. An important next step is to incorporate these impairments into the optimization problem.

Theory and practice perform differently as a result of these flaws, which hinder the ideal phase shift predicted by equations (3) and (7).

4.3. Scalability and Network Integration

For 6G systems, the model that is being presented takes into account a single IRS helping a single user. It is critical for scalability to multi-cell, multi-user, and multi-IRS scenarios. When you use more than one IRS, you run into problems like interference between surfaces, collaborative beamforming, and a combinatorial increase in the difficulty of optimization. We would need to use distributed or hierarchical optimization methods to make our current DS-PSO framework work with this level of complexity. Moreover, incorporating IRS control into current network protocols and standards (e.g., for handover and resource allocation) presents a systems-level challenge that must be resolved for seamless implementation.

4.4. Computational Complexity and Real-Time Operation

The DS-PSO algorithm is powerful, but it takes more time to compute than analytical solutions. It can only work in real time if the channel’s coherence time is long enough. For places where the signal fades slowly, the optimization can be done offline or with a slow refresh rate. We are actively working on developing low-complexity deep learning-based approximations of the optimization process that would work in high-mobility situations and make sure that the system responds in real time.

4.5. Environmental Obstacles and Deployment

It is very important to put IRSs in the right places, as our simulation setup (Figure 2) shows. Unforeseen barriers can sever the presumed Line-of-Sight (LOS) connections to the IRS. For practical use, careful planning for each site and the use of multiple distributed IRSs are needed to make sure that coverage is strong. The proposed model sets a limit on how well the system can work, but real gains will depend on careful deployment strategies that make it more likely that the LOS components will be strong.

4.6. Practical Constraints on Optimal LOS Gains

As rightly highlighted, the core of our optimized model relies on achieving the improved LOS channel gains ( $β_{s r}^{o}$ and $β_{r d}^{o}$ ) defined in Equation (33). Several practical constraints can limit the realization of these gains:

Placement and Obstructions: To get these best results, the IRS must be placed where there are no obstructions and where it can see both the source and the destination clearly. Finding the perfect spot in real-life situations, like urban canyons or crowded indoor spaces, is very hard. The assumed LOS paths can be readily broken by the presence of structures, vegetation, or even moving objects like cars, which would return the channel to a weaker NLOS state and significantly reduce the IRS’s benefit.

Site-Specific Planning: It takes extensive, site-specific radio planning to achieve βᵒ practically; it is not just a matter of geometry. Beyond the static, idealized assumptions of our model, intelligent and possibly adaptive deployment strategies are required to account for factors like material reflectivity, incidence angles, and the dynamic presence of new obstacles.

These limitations establish the crucial boundary conditions for reaching our anticipated performance rather than invalidating our findings. The authors emphasize that the theoretical gains are only a maximum and that their actualization depends on resolving these deployment issues by combining dynamic channel acquisition, robust beamforming, and IRS placement optimization.

As a result, we completely concur that these real-world issues are important and serve as the foundation for current IRS research. Our work establishes a theoretically optimized performance target under controlled conditions, which is an important first step. The notable improvements shown (such as 366 Mbit/Joule at 10-bit/s/Hz) warrant more research into resolving these real-world issues. Building directly upon the solid foundation established by this paper, the next stage of our research will specifically concentrate on integrating robust optimization under imperfect CSI, hardware constraints, and multiuser scalability.

5. Conclusions and Future Work

5.1. Conclusions

This study tackled the crucial problem of increasing energy efficiency (EE) in IRS-assisted 6G networks under high data rate circumstances by utilizing artificial intelligence (AI). To solve the non-convex optimization problem that comes with designing IRS phase shifts, we used an artificial intelligence (AI) framework as the main part of our method. We created and used a new hybrid Dynamic and Static Particle Swarm Optimization (DS-PSO) algorithm to smartly set up the IRS elements. The results from this AI-driven method show that our improved Intelligent Reflecting Surfaces (IRS) model is much better than standard IRS and SISO systems. At a data rate of 10 bits/s/Hz, it is up to 269% more energy efficient. ${I R S}^{o}$ is 46.4% better than Triple-IRS, which shows that optimization is better than hardware redundancy. Also, ${I R S}^{o}$ at very low data rates (≤0.01) works much better than IRS with PSO and IRS with GA. This suggests that hybrid optimization may be needed to improve energy efficiency. Consequently, it performs better than other AI-based optimizers that have been recently discussed, including multi-IRS configurations. The improved performance of the model at high data rates indicates that it can increase the data transmission efficiency of sixth-generation (6G) communication networks.

5.2. Future Work

In the future, we will verify the results and test the algorithm’s performance in more challenging environments, such as urban canyons with significant interference and non-line-of-sight (NLOS) components, using measured channel data from real-world scenarios.

The encouraging outcomes of our (DS-PSO- ${I R S}^{o}$ ) model provide a solid basis for a number of important research directions. The transition from theoretical models to reliable, workable implementations for 6G systems will be the main focus of our immediate future work, which will be structured along four main lines.

First, by substituting sophisticated stochastic models that take into consideration time-varying fading, shadowing, and random blockages for deterministic channels, we intend to expand our model to dynamic and complex environments. We will look into sophisticated Deep Reinforcement Learning (DRL) algorithms to handle this added complexity and allow for real-time adaptation. In the face of erratic interference and user mobility, these agents will be built to continuously learn and optimize IRS configurations.

The scalable integration of several IRSs in heterogeneous networks is the second thing we intend to look into. In order to develop "smart radio environments" for the entire network, this research will examine cooperative beamforming between surfaces and inter-IRS interference management. Additionally, we will look into how IRSs and Mobile Edge Computing (MEC) can work together to improve communication and computational energy efficiency by establishing advantageous connections for computational offloading.

Third, we will address practical hardware limitations and conduct experimental validation to close the gap between simulation and real-world implementation. Creating methods to reduce amplitude losses and phase quantization errors in metasurfaces will be part of this. The ultimate objective is to validate the anticipated energy efficiency and data rate gains under real-world conditions by designing a prototype and carrying out field trials in a controlled testbed.

Finally, the application of this work to MIMO systems is a logical and significant extension. In this case, the optimization problem gets a lot bigger because it has to do with both the active precoding/combining matrices at the transceivers and the passive phase shifts at the IRS. This makes it a coupled, high-dimensional, non-convex problem. We will investigate modifying the DS-PSO algorithm to encode a larger solution vector that encompasses all optimization variables, leveraging its exploratory capabilities to maximize the overall spectral or energy efficiency of the MIMO-IRS system. Concurrently, we will explore the application of more complex AI architectures, particularly DRL, to manage this joint active and passive beamforming optimization with lower latency, assessing its practical robustness against measured channel data from real-world scenarios.

List of Abbreviations

AI	Artificial Intelligence
CSI	Channel State Information
DS-PSO	Dynamic and Static Particle Swarm Optimization
EE	Energy Efficiency
IRS	Intelligent Reflecting Surface
LOS	Line of Sight
MIMO	Multiple-Input Multiple-Output
NLOS	Non-Line-of-Sight
PSO	Particle Swarm Optimization
RIS	Reconfigurable Intelligent Surface
SE	Spectral Efficiency
SISO	Single-Input Single-Output
SNR	Signal-to-Noise Ratio
UMi	Urban Micro (cell)
6G	Sixth-Generation

Author Contributions

Conceptualization, methodology, software: J.K.S.A.-S.; validation, formal analysis: A.T.R.A.; investigation, resources, data curation, design and creation of figures, writing—original draft preparation, writing—review and editing, visualization, supervision, project administration: J.K.S.A.-S. and A.T.R.A. All authors have read and agreed to the published version of the manuscript.

Availability of Data and Materials

All data supporting the findings of this study are included within the manuscript.

Consent for Publication

No consent for publication is required, as the manuscript does not involve any individual personal data, images, videos, or other materials that would necessitate consent.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

The study did not receive any external funding and was conducted using only institutional resources.

Acknowledgment

The authors would like to thank and acknowledge the use of MATLAB and Microsoft Office for simulations, figures, tables, and complete text preparation.

References

[1] X. Wang, J. Li, J. Wu, L. Guo, and Z. Ning, “Energy Efficiency Optimization of IRS and UAV-Assisted Wireless Powered Edge Networks,” IEEE J. Sel. Topics Signal Process., vol. 18, no. 7, pp. 1297–1310, 2024. [CrossRef]

[2] J. Li, Y. Huang, J. Wu, X. Wang, and Z. Ning, “Energy Efficiency Maximization for STAR-RIS and UAV-Assisted IUA: A Multi-Agent DRL Approach,” IEEE Internet Things J., vol. 12, no. 21, pp. 43936–43948, 2024. [CrossRef]

[3] J. Wang and S. Chen, “Deep Reinforcement Learning-Based Secrecy Rate Optimization for Simultaneously Transmitting and Reflecting Reconfigurable Intelligent Surface-Assisted Unmanned Aerial Vehicle-Integrated Sensing and Communication Systems,” Sensors, vol. 25, no. 5, p. 1541, 2025. [CrossRef]

[4] P. Vishwakarma, S. N. Sur, S. Dhar, and D. Bhattacharjee, “IRS-Assisted SWIPT: Power Optimization Strategies for Green Communications,” in presented at the 2025 17th International Conference on COMmunication Systems and NETworks (COMSNETS), Bengaluru, India, 6–10 Jan. 2025, pp. 356–364. [CrossRef]

[5] H. Sadia, H. Iqbal, and S. Qadir, “Physical Layer Security in Intelligent Reflecting Surface-Enabled Small NOMA IoT Network,” in presented at the 2024 11th International Conference on Wireless Networks and Mobile Communications (WINCOM), Leeds, UK, 23–25 July 2024, pp. 1–6. [CrossRef]

[6] Q. Wu, T. Lin, X. Yu, Y. Zhu, and R. Schober, “Beamforming for PIN Diode-Based IRS-Assisted Systems Under a Phase Shift-Dependent Power Consumption Model,” IEEE Trans. Commun., vol. 73, no. 9, pp. 8092–8109, 2025. [CrossRef]

[7] W. Fang, W. Chen, Q. Wu, X. Zhu, Q. Wu, and N. Cheng, “Channel Characterization of IRS-Assisted Resonant Beam Communication Systems,” IEEE Trans. Commun., vol. 73, no. 9, pp. 7381–7397, 2025. [CrossRef]

[8] P. Siddhartha, L. Yashvanth, and C. R. Murthy, “Exploiting Beam-Split in IRS-Aided Systems via OFDMA,” in presented at the ICASSP 2025-2025 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Hyderabad, India, 6–11 Apr. 2025, pp. 1–5. [CrossRef]

[9] Y. Chen, Q. Wu, G. Chen, and W. Chen, “Spatial Multiplexing Oriented Channel Reconfiguration in Multi-IRS Aided MIMO Systems,” IEEE Trans. Veh. Technol., vol. 74, no. 6, pp. 9840–9845, 2025. [CrossRef]

[10] M. Maashi, et al., “Energy Efficiency Optimization for 6G Multi-IRS Multi-Cell NOMA Vehicle-to-Infrastructure Communication Networks,” Comput. Commun., vol. 225, pp. 350–360, 2024. [CrossRef]

[11] J. Zhao, Q. Zhang, T. Ai, X. Wei, and F. Peng, “Optimal Reconfigurable Intelligent Surface Deployment for Secure Communication in Cell-Free Massive Multiple-Input Multiple-Output Systems with Coverage Area,” Electronics, vol. 14, no. 2, p. 241, 2025. [CrossRef]

[12] S. Sivasankar and S. Markkandan, “Fast and Scalable Intelligent Reflecting Surface Beamforming Using Hybrid Learning Approaches,” IEEE Access, vol. 13, pp. 152826–152842, 2025. [CrossRef]

[13] M. A. Ahmed, A. Baz, and M. M. Fouda, “Polyhedron Optimization for Power Allocation of Cell-Free Based IRS System,” IEEE Access, vol. 12, pp. 76065–76073, 2024. [CrossRef]

[14] A. Khaled, A. S. Alwakeel, A. M. Shaheen, M. M. Fouda, and M. I. Ismail, “Placement Optimization and Power Management in a Multiuser Wireless Communication System with Reconfigurable Intelligent Surfaces,” IEEE Open J. Commun. Soc., vol. 5, pp. 4186–4206, 2024. [CrossRef]

[15] K. Wang, P. Liu, K. Liu, L. Chen, H. Shin, and T. Q. S. Quek, “Joint Beamforming and Phase-Shifting Design for Energy Efficiency in RIS-Assisted MISO Communication with Statistical CSI,” Phys. Commun., vol. 59, p. 102080, 2023. [CrossRef]

[16] H. Hashida, Y. Kawamoto, and N. Kato, “Mathematical Modeling and Deployment Optimization: Intelligent Reflecting Surface-Aided Communications Under Partial Blockages,” IEEE Trans. Cogn. Commun. Netw., vol. 11, no. 5, pp. 3306–3316, 2025. [CrossRef]

[17] G. D. Verma, A. Mathur, Y. Ai, and M. Cheffena, “Mixed Dual-Hop IRS-Assisted FSO-RF Communication System with H-ARQ Protocols,” IEEE Commun. Lett., vol. 26, no. 2, pp. 384–388, 2021. [CrossRef]

[18] A. Sikri, A. Mathur, and G. Kaddoum, “Joint Impact of Phase Error, Transceiver Hardware Impairments, and Mobile Interferers on RIS-Aided Wireless System Over κ-μ Fading Channels,” IEEE Commun. Lett., vol. 26, no. 10, pp. 2312–2316, 2022. [CrossRef]

[19] C. Lai and R. Zhao, “An Autocorrelation-Based r-Stability Condition With Application in the Design of IIR Filters,” IEEE Signal Process. Lett., vol. 31, pp. 1389–1393, 2024. [CrossRef]

[20] J. Li, J. Liu, and J. Wang, “Optimizing Spectrum and Energy Efficiency in IRS-Enabled UAV-Ground Communications,” Comput. Netw. Jan., vol. 256, p. 110911, 2025. [CrossRef]

[21] A. T. Alsahlanee, “Convergence Rate For Low-Pass Infinite Impulse Response Digital Filter,” J. Phys. Conf. Ser. Jul., vol. 1963, no. 1, p. 012103, 2021. [CrossRef]

[22] A. T. R. Alsahlanee and J. K. S. Al-Safi, “Improving Channel Gain of 6G Communications Systems Supported by Intelligent Reflective Surface,” Indones. J. Elect. Eng. Inform. (IJEEI), vol. 13, no. 1, pp. 57–68, Feb. 2025. [CrossRef]

[23] J. Singh, N. A. Shelke, D. S. Hasan, M. Sajid, A. T. R. Alsahlanee, and K. Upreti, “Enhanced Learning in IoT-Based Intelligent Plant Irrigation System for Optimal Growth and Water Management,” in presented at the International Conference on Intelligent Systems Design and Applications, Olten, Switzerland, 11–13 Dec. 2023, pp. 231–240. [CrossRef]

[24] J. K. S. Al-Safi and C. Kaleli, “A Correlation and Slope-Based Neighbor Selection Model for Recommender Systems,” in presented at the Next Generation of Internet of Things: Proceedings of ICNGIoT 2021, Odisha, India, 5–6 Febr. 2021, pp. 243–268. [CrossRef]

[25] J. Al-Safi and C. Kaleli, “Item Genre-Based Users Similarity Measure for Recommender Systems,” Appl. Sci., vol. 11, no. 13, p. 6108, 2021. [CrossRef]

[26] P. K. Keer, J. K. S. Al-Safi, S. B. G. T. Babu, and G. Ramesh, “Artificial Intelligence in Computer Network Technology in The Big Data Era,” in presented at the 2022 5th International Conference on Contemporary Computing and Informatics (IC3I), Uttar Pradesh, India, 14–16 Dec. 2022, pp. 2131–2135. Available: https://alochana.org/wp-content/uploads/50-AJ3257.pdf

[27] E. Björnson, Ö. Özdogan, and E. G. Larsson, “Intelligent Reflecting Surface Versus Decode-and-Forward: How Large Surfaces Are Needed to Beat Relaying?,” IEEE Wireless Commun. Lett., vol. 9, no. 2, pp. 244–248, 2019. [CrossRef]

[28] Ö. Özdogan, E. Björnson, and E. G. Larsson, “Intelligent Reflecting Surfaces: Physics, Propagation, and Pathloss Modeling,” IEEE Wireless Commun. Lett., vol. 9, no. 5, pp. 581–585, 2019. [CrossRef]

[29] Q. Wu and R. Zhang, “Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming,” IEEE Trans. Wireless Commun., vol. 18, no. 11, pp. 5394–5409, 2019. [CrossRef]

[30] J. Wang, H. Yang, Z. Wang, and C. Li, “MDRD-Based Channel State Information Acquisition Scheme for Intelligent Reflecting Surface-Aided Wireless Communication Systems,” Phys. Commun., vol. 71, p. 102667, 2025. [CrossRef]

[31] Z. Q. He and X. Yuan, “Cascaded Channel Estimation for Large Intelligent Metasurface Assisted Massive MIMO,” IEEE Wireless Commun. Lett., vol. 9, no. 2, pp. 210–214, 2019. [CrossRef]

[32] D. Tyrovolas, et al., “Energy-Aware Trajectory Optimization for UAV-Mounted RIS and Full-Duplex Relay,” IEEE Internet Things J., vol. 11, no. 3, pp. 24259–24272, 2024. [CrossRef]

[33] C. Y. Goh, C. Y. Leow, and R. Nordin, “Energy Efficiency of Unmanned Aerial Vehicle with Reconfigurable Intelligent Surfaces: A Comparative Study,” Drones, vol. 7, no. 2, pp. 1–17, 2023. [CrossRef]

[34] E. Björnson and L. Sanguinetti, “Demystifying the Power Scaling Law of Intelligent Reflecting Surfaces and Metasurfaces,” in presented at the 2019 IEEE 8th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Le Gosier, Guadeloupe, 15–18 Dec. 2019, pp. 549–553. [CrossRef]

[35] D. Bratton and J. Kennedy, “Defining a Standard for Particle Swarm Optimization,” in presented at the 2007 IEEE Swarm Intelligence Symposium, SIS 2007, Honolulu, HI, USA, 1–5 Apr. 2007, pp. 120–127. [CrossRef]

[36] J. Kennedy and R. Eberhart, “Particle Swarm Optimization,” in presented at the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 Nov.–1 Dec. 1995, pp. 1942–1948. [CrossRef]

[37] D. Sanchez, “DS-PSO: Particle Swarm Optimization with Dynamic and Static Topologies. Bowdoin College, Bowdoin Digital Commons, Honors Projects, 2017,”. [Online]. Available: https://digitalcollections.bowdoin.edu/view/5093 (Accessed: 1 May 2017)..

[38] GPP, “Further Advancements for E-UTRA Physical Layer Aspects (Release 9). 3rd Generation Partnership Project (3GPP), Technical Report 36.814, 2010,”. [Online]. Available: https://api.semanticscholar.org/CorpusID:16652630 (Accessed: 1 Nov. 2025)..

[39] S. Penchala, S. K. Bandari, V. V. Mani, and A. Drosopoulos, “Controlled Wireless Channel using Multi-Antenna Multi-IRS Assisted Communication System: A Comprehensive Performance Analysis,” IEEE Latin America Trans., vol. 23, no. 2, pp. 114–124, 2025. [CrossRef]

[40] H. Nguyen-Thi, T. Kieu-Xuan, T. Le-Nhat, and A. Le-Thi, “Improving Energy Efficiency for Intelligent Reflecting Surface Assisted PD-NOMA in EH Relaying Network,” J. Inf. Telecommun., pp. 1–24, 2025. [CrossRef]

Computing&AI Connect

Table of Contents